To the previous case study: Kelvin-Helmholtz instability
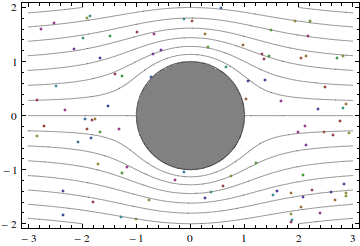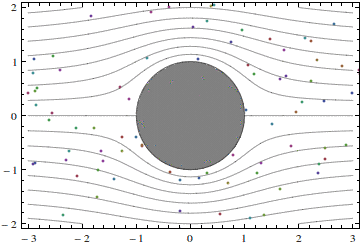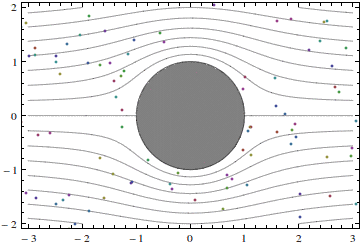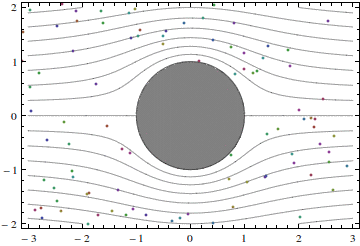
In reality, the fluid flows past cylinders are never potential. On the other hand, understanding potential flows is crucial for understanding real flows. Hence, just have a look at what a potential flow past a circular cylinder is like:
Notice the following features.
Solid lines in the picture are streamlines. The flow is steady, and the fluid particles never go across the streamlines. This, of course, is the feature of all steady flows.
There are two stagnation points, a forward stagnation point and a rear stagnation point. A stagnation point is such a point that fluid particle velocity slows down to zero when the particle approaches the stagnation point. In the flow shown in the picture these points are at the crossing of the horizontal symmetry axis and the cylinder surface.
The flow also has a vertical symmetry axis, passing through the center of the cylinder. This is only possible for bodies that have such a symmetry, and even for a symmetric body the real flow would not have a vertical symmetry axis: this is the feature specific to potential flows and so-called Stokes flow, which are flows at very small Reynolds numbers.
Near the top and the bottom of the cylinder the particle velocity is the highest. This can be seen directly from the animation, or inferred from the small cross-section of the streamtube, which is the region between two streamlines.
The particles accelerate from the stagnation point towards the top of the cylinder. This acceleration is caused by pressure difference: the pressure at the top is smaller than the pressure at the stagnation points.
The particles go around the curved cylinder surface. To deflect them from going along a straight line, they should be pushed towards the cylinder surface. This is done by the pressure.
The velocity of this flow is given by a simple explicit formulas:
u = U [1 − (x2 – y2)a2/(x2 + y2)2 ], v = −2Uxya2/(x2 + y2)2 .
where x and y are the horizontal and vertical coordinates in the flow, u and v are the corresponding velocity components, a is the cylinder radius, and U is the horizontal velocity component far upstream. The vertical velocity component far upstream is zero, which can always be achieved by selecting the x axis to be along the flow direction far upstream.
The pressure p is given by the Bernoulli equation, p = Const – ρ (u^2 + v^2)/2, where ρ is the fluid density. In potential flows the constant Const is the same at all points in the flow.
To the next case study: Asymmetric potential flow past a cylinder