To the previous case study: Symmetric potential flow past a cylinder

Figure 1. U = 0, Γ  = π.

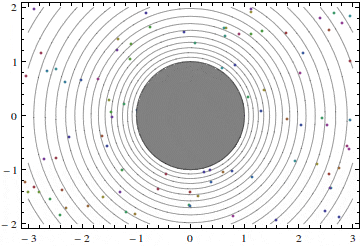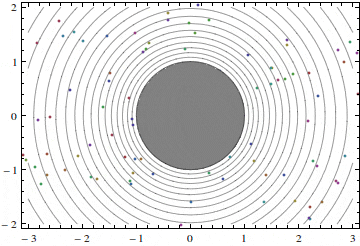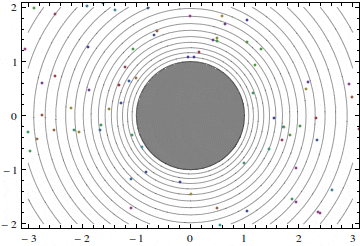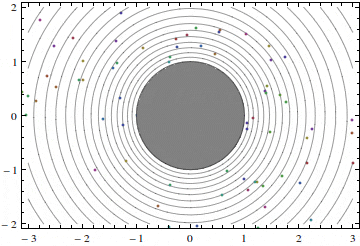
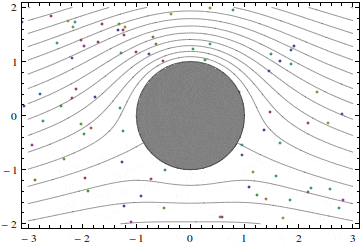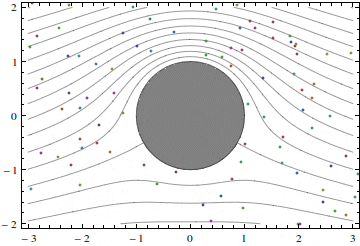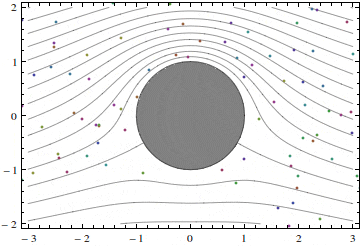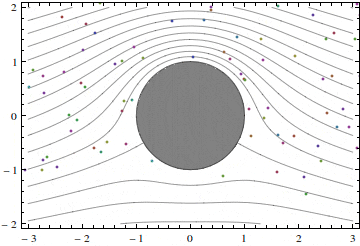
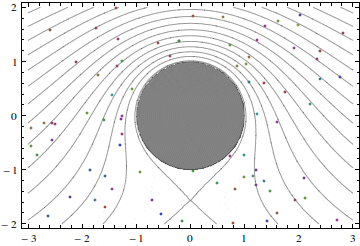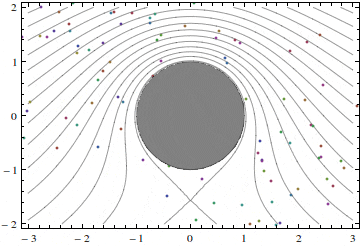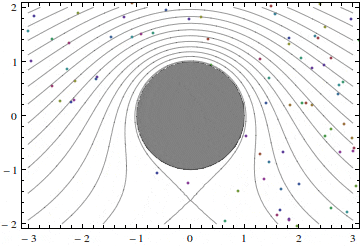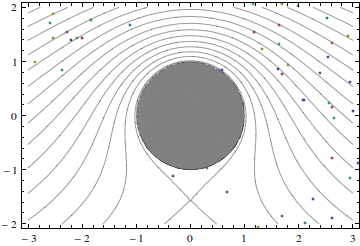
A potential flow past a cylinder with an up/down symmetry is unique, up to rescaling of the velocity and coordinates to make the diameter of the cylinder the same and the velocity at infinity the same in all cases. If, however, the flow is allowed to be asymmetric (that is not symmetric), other solutions are also possible. One such solution is shown in figure 1. Here, the streamlines are just circles co-centered with the cylinder, and the fluid particles move around the cylinder. The magnitude w of the velocity of this motion is inversely proportional to the distance to the center of the cylinder: w =Γ/(2πr). One can see that Γ is the product of the velocity magnitude and the length of the circle, and that Γ is the same for all streamlines. Quantity Γ is called circulation, and circulation can be defined for any flow and for any closed contour and not only for a circle, but we will not do it here even though the notion of circulation is important. Here, we only note that Γ serves as a parameter in this flow: we can prescribe it any value we wish. The velocity components of this flow are

u=(Γ/π)(y/(x²+y²),            v= -(Γ/π)(x/(x²+y²).

(Exercise: recollect that potential flows are flows with zero vorticity, that vorticity is the angular velocity of infinitely short mutually-perpendicular material lines, select a group of material points in the figure and watch them move. Does the group rotate? How is this related to the velocity behaving like 1/r?)

Figure 2. U = 1, Γ = π

Using the superposition principle, we can add together the velocities of the symmetric flow past a cylinder and the velocity of the flow considered here, to obtain

u = U [1 − (x² – y²)a²/(x² + y²)² ] + (Γ/π)(y/(x²+y²),

v = −2Uxya²/(x² + y²)²   -(Γ/π)(x/(x²+y²).

Here, a stands for the cylinder radius.

Figure 3. U = 1, Γ = 2.2π

Figures 2 and 3 show two such flows with different values of the velocity at infinity U and circulation Γ.

In general, a 2-dimensional potential flow past an arbitrary (but simply-connected) body, for example, the flow past an aerofoil, depend on two parameters, the velocity at infinity and the circulation. In the more general case the definition of circulation is also generalised, but we will not discuss this here.

A word of caution: because of the phenomenon of separation real flows past a cylinder almost never resemble the potential flows described here, except the case of quickly rotating cylinders. If the velocity of the cylinder surface is several times greater than the velocity at infinity, the real flow might be close to that shown in figure 3 (but with greater circulation).

To the next case study: Separated flows overview