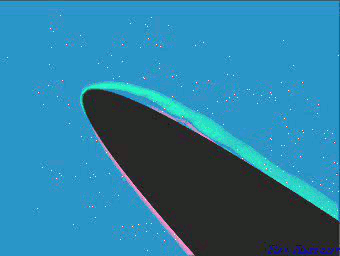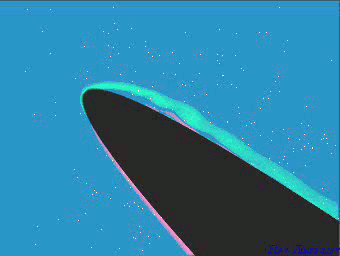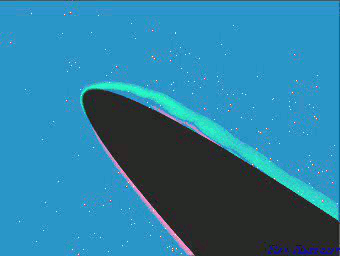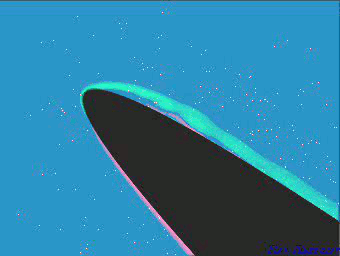To the previous case study: Bathtub vortex.
Kelvin-Helmholtz instability is very common. To understand it without mathematics it suffices to know vorticity dynamics.
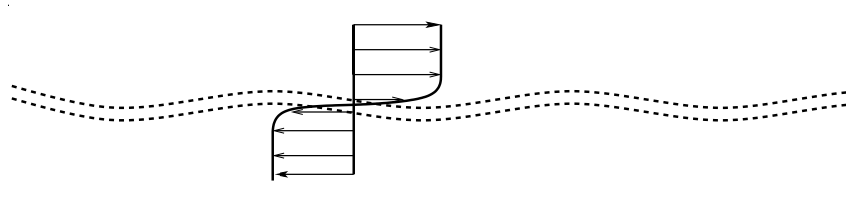
Consider a thin infinite horizontal layer of negative vorticity. For symmetry, let the velocity above and below the layer to be equal and of opposite directions. Let this layer to be sinusoidally perturbed as it is shown in this figure:
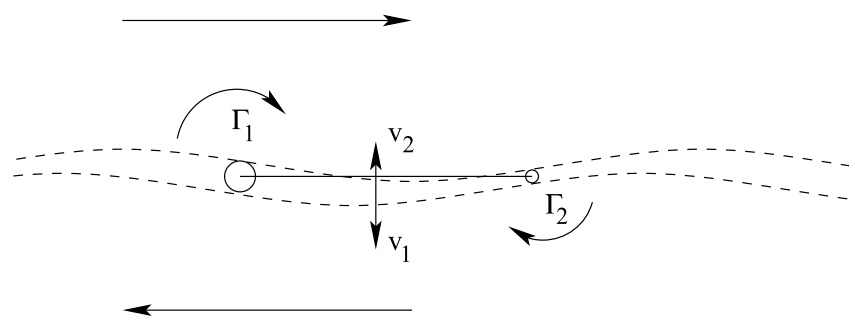
Then the flow carries (advects) the upper boundary of the layer to the right, while the lower boundary of the layer is advected to the left. As a result, the layer thickness will decrease where the layer slope is positive and increase where the layer slope is negative, resulting in the shape shown in this figure:
The rate with which the thickness is varying depends on the amplitude of the perturbation: the higher the amplitude the greater the rate of thickness variation (consider that for zero perturbation amplitude the thickness remains constant).
The section of the layer with higher thickness will now induce higher velocity than the section with smaller thickness. As the result, the amplitude of the sinuous disturbance will grow (because v1 is greater than v2). That, in turn, increases the growth rate of the thickness variation, and so on. This process is called Kelvin-Helmholtz instability. Viscosity can prevent this type of instability but only for not too large Reynolds numbers.
In practice this flow is often superimposed with a uniform flow, so that the wavy shear layer is moving downstream while the waves are growing in amplitude. This can be observed in this movie:
The movie shows marginal separation in the vicinity of the leading edge of an aerofoil. Kelvin-Helmholtz instability develops in the shear layer at the boundary of the separation region.
To the next case study: Symmetric potential flow past a cylinder