This page of our website is stand-alone. Bits and pieces of this page may be repeated in other pages. The goal here is to give the very first glimpse of the big picture of fluid dynamics. Only a general outline of the main fluid flow features is given. Glide over this: much will be explained later.
Reynolds number
A fluid flow past the body of the same shape can be of quite different character depending on other parameters, such as the size of the body, the average flow speed, fluid density and viscosity. Remarkably, fluid flows can be classified in terms of their dimensionless Reynolds number Re that is the product of the characteristic size of the body D and the characteristic velocity U, divided by the kinematic viscosity ν: Re = DU/ ν. Depending on the value of the characteristic Reynolds number, the flow past the same body can be steady or unsteady, laminar or turbulent, attached or separated.
For small, that is less than 1, values of Re the flows are typically steady, and more often than not attached. However, flows with small Re are less frequently encountered in practice. Consider the flow of air induced by a walking man. Take the characteristic dimension of a human as 1 meter and the characteristic walking speed as 5 km/h. At normal conditions the air kinematic viscosity is about 1.5×10-5m/s. Hence, for this case the characteristic Re is just above 92000. Since Re is proportional to the velocity and the size, for anything of a larger size or moving in the air faster Re will be even greater. The kinematic viscosity of water is about 10 times smaller than that of air, and, hence, for the same size and speed in water Re would be about 10 times larger. In human-related applications, therefore, large Re are typical, and we will pay more attention to this case.
Separation
Apart from the Reynolds number, the main factor determining the nature of the flow is the body shape. Shapes can be streamlined or bluff. A typical airfoil at a small angle of attack is a streamlined body, but at a very large angle of attack it is a bluff body. The difference between streamlined and bluff bodies is that the flows past streamlined bodies remain attached even at high Re, while flow past bluff bodies become separated as Re increases.
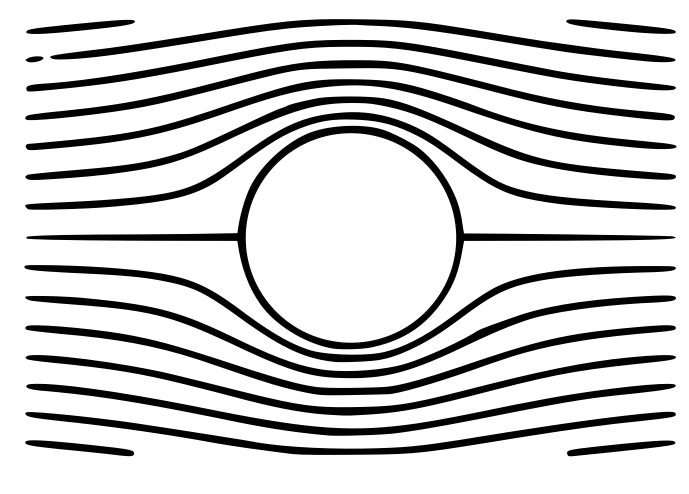
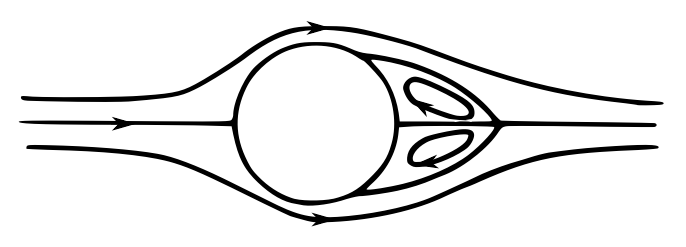
Telling a separated flow from a non-separated flow when one sees it is relatively easy. A characteristic feature of separated flows is flow reversal, that is the presence of a region, called a separation eddy, where the fluid moves in the direction opposite to the main direction of the flow. For example, the flow in figure 1 is attached, but the flow in figure 2 is separated.
Figure 1
Majority of separated flows encountered in practice are unsteady even at relatively small Re. For example, as Re (based on the diameter) increases beyond 50, the steady flow becomes unstable and evolves into a time-periodic flow, in which the eddies detach alternately from the sides of the cylinder and move downstream forming a structure called a von Karman vortex street, see figure 3.
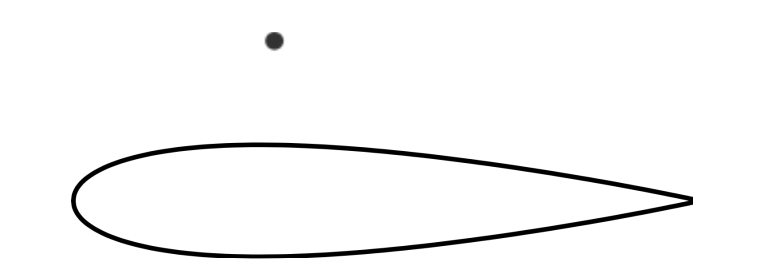
Separation is an important phenomenon. Figure 4 shows an airfoil and circular cylinder (the small black dot) that experience equal drag at very high Reynolds numbers. The huge difference in size is due to the flow being separated in the cylinder case and attached in the case of an airfoil.
Instability, transition, and turbulence
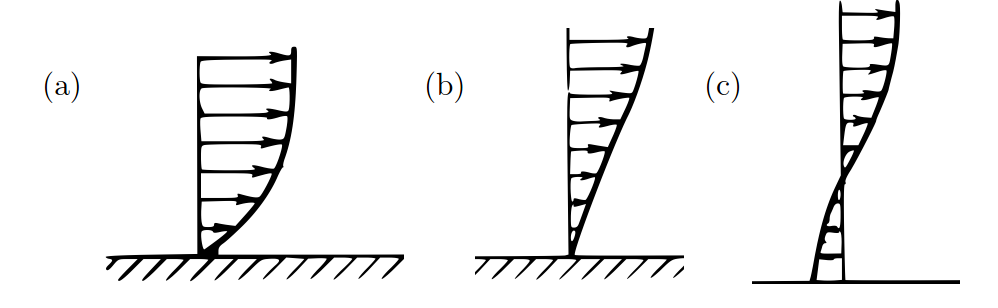
As the Reynolds number increases steady attached flows also loose stability and become unstable. This usually happens at much larger Re than in the case of a separated flow. The primary reason for this is the shape of the velocity profile. In general, flows with velocity profiles without inflection points, as in figure~5 (a), are much more stable than the flows with inflection points, as in figures 5 (b,c). The difference in the critical value of Re at which stability is lost in flows with and without inflection points varies, but typically it is more than an order of magnitude (more than 10 times).
In the flow past a circular cylinder for yet higher Re the regular vortex shedding becomes irregular, chaotic, and the spatial pattern of the flow also becomes irregular, disordered, eventually resulting in the so-called turbulent flow regime. Turbulent flows are characterized by simultaneous presence of many temporal and spatial scales, including very small scales, high energy dissipation due to the presence of those small scales, and by high sensitivity of the instantaneous flow features. Attached flows often do not exhibit a time-periodic behavior. Instead, if the steady flow is unstable, the flow becomes turbulent. Turbulent flows can easily be distinguished by the irregularity of the flow visualizations, by their chaotic time-dependent behavior and by the noise they are producing.
Boundary layers
Formation of boundary layers at high Re is one of the most important features of fluid flows. From the physical viewpoint, Reynolds number is the ratio of the average magnitudes of inertia and viscous friction in the bulk of the flow. If Re is high one could, therefore expect to be able to neglect the friction inside the fluid. However, without friction the fluid would slide along the solid walls bounding it, while in reality the fluid velocity is always equal to the velocity of the solid at their interface. Thus, at high Re a thin layer of fluid adjacent to the solid wall develops high velocity gradients, with the velocity varying from the wall velocity at the wall to the velocity in the bulk of the flow. This thin layer is called a boundary layer. Boundary layers can be laminar or turbulent, and they can separate from the surface and continue into the bulk of the fluid in the form of so-called mixing layers. Discussion of boundary layers will be continued once the quantity called vorticity will be introduced.
Drag of various bodies
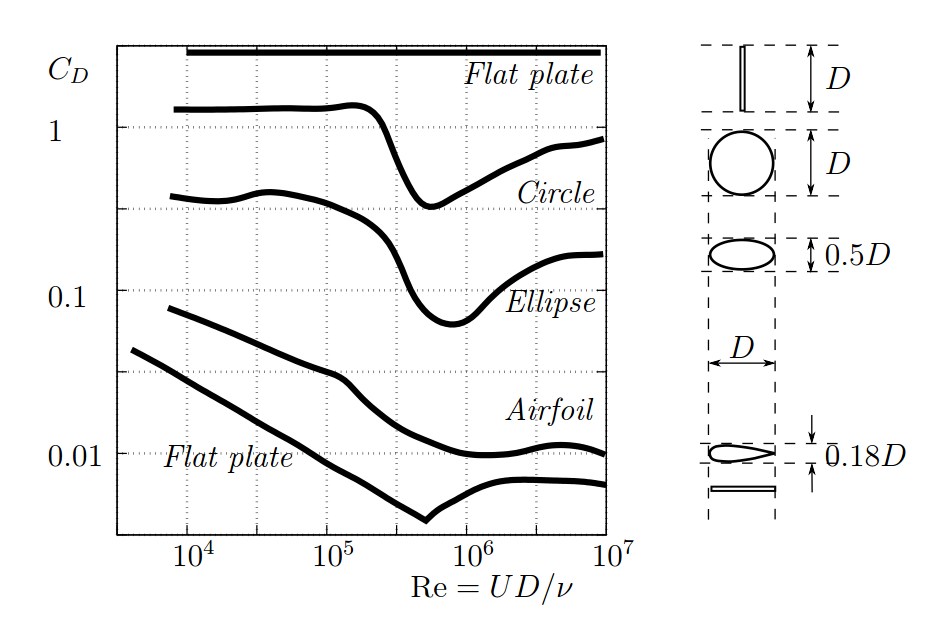
In conclusion of this overview, we give also a summary plot of drag of various bluff and streamlined bodies (figure 6). For interpreting this plot it is convenient to assume that the flow at infinity and the body size are fixed. Then the drag coefficient CD is proportional to the drag, and an increase in Re corresponds to a decrease in viscosity. Note the logarithmic scales and note the range of Re displayed.
The bottom curve in figure 6 is for a thin flat plate parallel to the main flow direction. For smaller Re the flow is laminar, and decrease in viscosity leads to a decrease in the drag, as it can be expected. At Re somewhat below 1000000 a transition to turbulence occurs. The drag then increases with a decrease in viscosity (increase in Re) until the transition effect saturates. After that, further decrease in viscosity reduces the drag, but at a much slower rate than for the laminar flow.
The top curve in figure 6 is for a thin flat plate perpendicular to the main flow direction. In this case the sharp edges of the plate cause flow separation, which is a very powerful feature dominating the flow. The drag is high and independent of Re.
The curve for a circular cylinder (circle) exhibits an interesting phenomenon called drag crisis. Somewhere between Re=100000 and Re=1000000 the drag coefficients drops as Re increases. This happens when the boundary layer on the cylinder surface undergoes transition to turbulence. Turbulent boundary layers are more resistant to separation, and as a result the separation region shrinks, decreasing the drag.
The drag curves of the ellipse and the airfoil have a behaviour intermediate of that for the circle and the flat plate aligned with the flow.