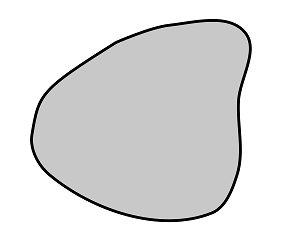
Suppose that we are considering a potential flow inside a region shown in the figure. An important question is how many different potential flows inside this region are possible. The answer is: an infinite number. To decide which flow is the one that actually will happen (given that we know that the flow is indeed potential) one uses boundary conditions. For potential flows the most common boundary condition is that which prescribes the velocity component perpendicular to the boundary. It can be proven mathematically that for any given distribution of the normal velocity on the boundary there is only one potential flow, but only if a certain condition on the shape of the region is satisfied. Namely, for this statement to be true, the region should be simply-connected.
Figure 1. Simply-connected region.
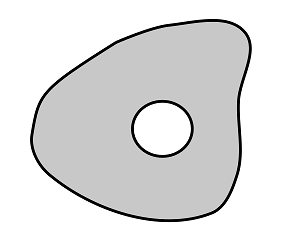
A region is simply-connected if any closed curve drawn inside the region can be shrunk to a point continuously while remaining in the region. Thus, the region in figure 1 is simply-connected while the region in figure 2 is not. Indeed, if the curve encloses the hole in the region then no continuous deformation can shrink it to a point without leaving the region at least for some time during this deformation.
Figure 2. Multiply-connected region.
The uniqueness of potential flows in simply-connected domains together with the superposition principle implies an important property of potential flows. Namely, if the normal velocity component of a potential flow is zero everywhere on the boundary then it is zero everywhere in the entire region. Indeed, if this were not so one could always superimpose this flow on any flow with the non-zero normal velocity and thus obtain at least two potential flows satisfying the same boundary condition.
If the region is not simply-connected then prescribing the normal velocity on the boundaries is not enough to make the potential flow unique. We will consider what happens in multiply-connected regions later. Meanwhile, to get a first glimpse into the question, explore the potential flows in the Case Studies.