Vorticity is one of the most important and most useful notions in fluid dynamics.
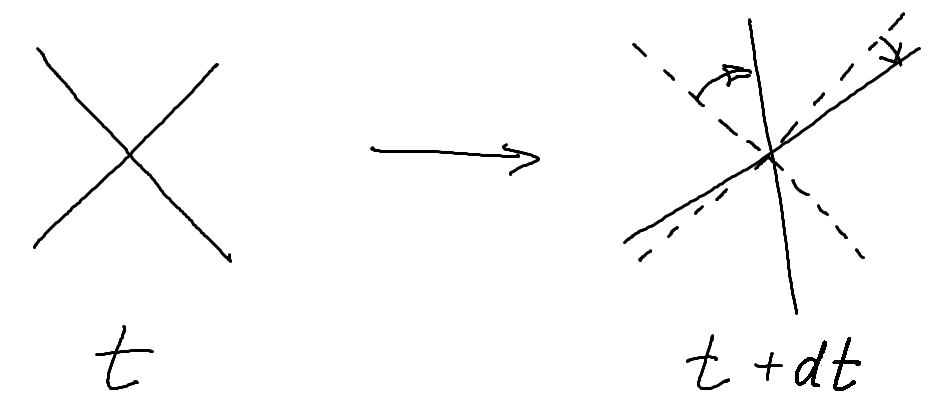
Vorticity is the angular velocity of fluid particles multiplied by 2. It is easier to explain it first for two-dimensional flows. Let us mark fluid particles along a segment of a line and follow the motion of these particles. Such a line is called a material line. Our material line will be translated, rotated, and bent. If the segment length is very small, bending can be neglected, and we come to an idea of the angular velocity, that is the speed of rotation of such a small segment. In a solid body this would be enough. Fluid, however, can also undergo deformation. As a result, two intersecting material lines might have different angular velocities, as it is illustrated in the figure.
Then, what can be called an angular velocity of the fluid at the point of intersection of these two material lines?
The answer is that one should only take mutually-perpendicular material lines. Then it can be proved mathematically that the sum of the angular velocities of the lines does not depend on the orientation of those lines. This sum is called vorticity.
Note that if the angular velocities of these two segments are different then they can become perpendicular only for an instant, and only at that instant the sum of the angular velocities equals vorticity.
In the general three-dimensional case angular velocity is a vector. A solid body rotation has an axis, the direction of which is the direction of the vector of angular velocity, while the speed of rotation is the magnitude of this vector. Let us now draw three mutually perpendicular segments of material lines through the same point in the fluid. Then the sum of the angular velocities at which any two of these lines rotate around the third line is the vorticity component along that third line.
Note that in three-dimensional case material lines can be stretched by the flow. This is important, but does not change the definition of vorticity.
In Flow Illustrator large positive and large negative values of vorticity are marked with colour. Watching a number of videos and observing the relationship between vorticity and the snowflake motion will help to develop the intuitive understanding of this relationship.
If the vorticity distribution is known then after some training it is possible to imagine the corresponding velocity distribution. Note that even when the vorticity is everywhere zero a fluid motion is possible. Such flows are called irrotational or potential. There are effective mathematical tools for studying such flows, and they too yield to simple intuitive interpretation.
The reason why vorticity is important in fluid dynamics is that its behaviour is easy to understand at an intuitive level. In standard textbooks on fluid dynamics it is demonstrated that if the action of viscosity can be neglected then the vorticity vector behaves as an element of a material line: it is advected (that is carried by the fluid), rotated, and stretched.
In case of a two-dimensional flow the vorticity has only one component perpendicular to the plane of the flow, and hence it cannot be stretched or rotated. Watching Flow Illustrator videos for large Reynolds numbers, say, above 1000, one can notice that coloured areas often move with fluid particles.
The effect of viscosity is equivalent to diffusion of vorticity in the fluid, in addition to advection. This effect is also easy to understand intuitively. It is most clearly observed in flows with boundary layers.