Another type of force acting inside the fluid is friction. Our everyday experience suggests that, unlike pressure, friction is small in air and water. Place the palm of your hand on the surface of the table and move your hand back and forth. Feel the friction force. Then lift the hand and move it in the air: the air friction is imperceptible. If so, should one pay attention to it? The answer is a very definite yes. Explaining why small friction has a large effect will take more than one page. In this page we will discuss friction in a very simple case.
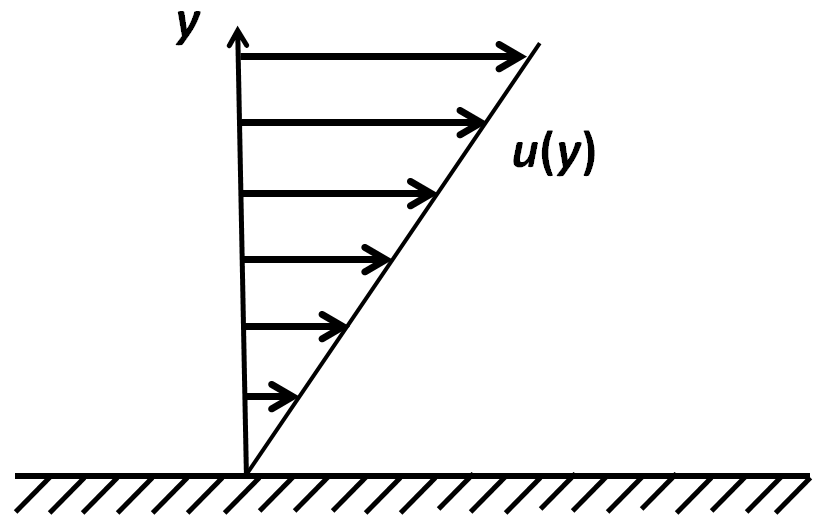We will consider first the simple case when the velocity vectors have the same direction everywhere, while the magnitude of the velocity varies linearly in the direction perpendicular to the direction of the velocity. This frequently happens in the vicinity of a wall as is illustrated in the figure, showing a velocity profile of a simple shear motion near a wall.
Such a flow is called a shear flow because of the shearing motion of the fluid layers which slide past one another.
In this case the friction force exerted on the wall will be proportional to the shear rate, which in this case can be calculated as the derivative of u with respect to y, that is du/dy, and since the velocity profile is linear, and the velocity at the wall is zero, this is simply u(y)/y. The force τ exerted on the unit area of the wall is given by the formula
τ=μ du/dy,
where the constant μ, called the viscosity coefficient, depends on the fluid. Its numerical value can be found in handbooks, and it usually depends on the temperature. The above formula is called Newton’s viscous friction law. The same formula remains valid inside the fluid. In that case it gives the force exerted on one another by the layers of moving fluid.
Friction in more complicated flows is discussed in a separate page. However, the simple description given here is useful in many particular cases.