When thinking about fluid flows, fluid dynamicists use special terminology: velocity field and pressure field, fluid particles, material lines, streamlines and streak lines, vorticity, Eulerian and Lagrangian viewpoints and many more. These terms constitute the language, the basic words of which need to be understood first. We will explain a few of these notions now.
Continuum
Fluid, as almost all other things, consists of molecules separated by empty space. Usually the mean free path, that is the average distance the molecules travel between collisions, is much smaller than the characteristic dimensions of the flow. Then it is convenient to imagine that the fluid mass is continuously distributed in space. This approach is common and is called continuum mechanics.
Characteristic dimensions or characteristic scales
Characteristic dimensions and scale are the relevant dimensions and scales. Knowing characteristic scales gives meaning to the words ‘small’ and ‘large’. Is 1 mm small? This depends on what it is to be compared with. Compared to the size of a car 1 mm is very small, but compared to the size of a virus it is very large. And compared to the size of a rain drop 1 mm is neither large nor small.
For example, for an aircraft the characteristic length can be taken as the length of the aircraft, and the characteristic velocity can be taken as the flight velocity. The characteristic time can be obtained as the characteristic length divided by the characteristic velocity. The exact values of the characteristic scales can be selected with a certain freedom provided that they remain physically relevant to the flow in question. The Reynolds number becomes physically meaningful when it is calculated with characteristic scales .
Fluid particle
Considering fluid as a continuum allows us to choose an arbitrary point in fluid and speak about fluid properties at this point, such as velocity and pressure. If the point keeps moving with the fluid velocity at this (moving) point then we call it a fluid particle. A fluid particle is, therefore, a model of a fluid volume very small as compared to the characteristic flow dimension (so that the size of this volume can be neglected) but very large as compared to the free path.
In movies made with Flow Illustrator randomly chosen fluid particles are shown as white dots. Watch a movie from the Gallery and observe the motion of the fluid particles.
Material line
Let us imagine a curve in space and mark all the fluid particles on this curve. The particles can move with time and so will do the curve formed by these particles. Such a curve moving with the fluid is called a material line. Fluid motion can translate material line, rotate it, stretch and bend it, so that the motion of a material line can be quite complicated.
Velocity field
Every fluid particle has its own velocity. Since fluid particles fill the entire space occupied by the fluid, fluid velocity is a field. It is often denoted as u(x), to emphasize that the velocity vector u depends on the position of the fluid particle. The position is determined by the vector x, which is a vector going from the coordinate origin to the point in question. Vectors are denoted by bold letters.
Streamlines
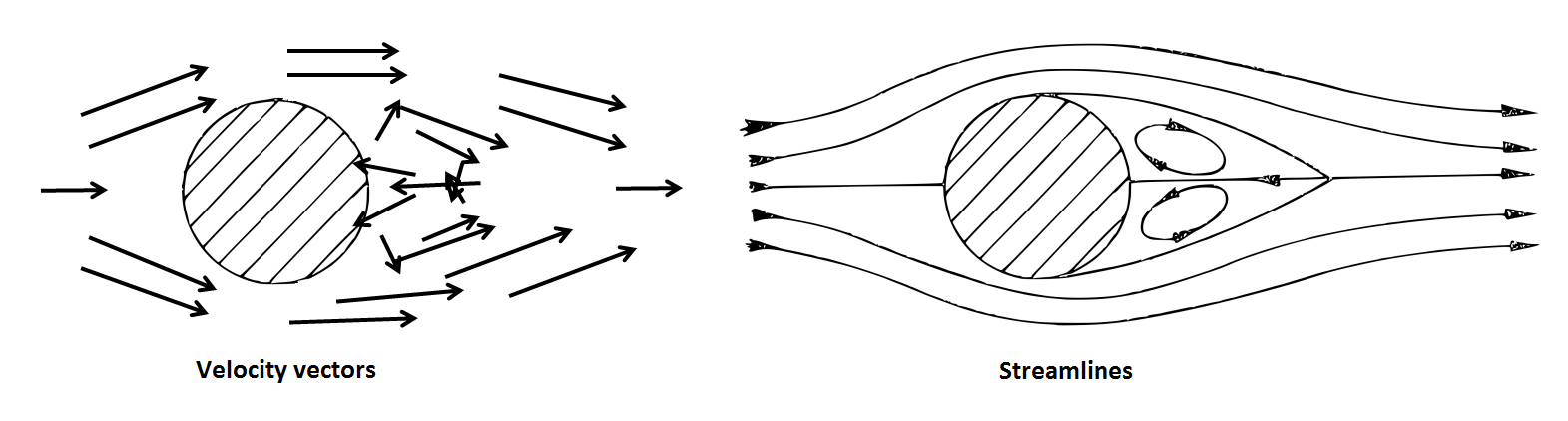To visualise the flow one can try to select a number of points in it, and at each point to draw the velocity vector of the corresponding fluid particle. Often, however, the result is difficult to understand. Instead, one can draw a set of curves along the direction of velocity. Such curves are called streamlines. The figure illustrates the advantage of visualising flows with streamlines. It shows a sketch of a separated flow past a circular cylinder at the value of the Reynolds number Re of about 20.
Planar and two-dimensional flows
The flow in the figure is shown as a flat image. Strictly speaking this is only possible if the velocity vectors lay in the plane of the picture, and it also implies that in the real three-dimensional world the velocity is the same at all points along the lines perpendicular to the plane of the picture. This is why the flow in the picture is the flow past a circular cylinder: what is shown is only one cross-section of the flow, and this is enough since it would be the same in all other cross-sections. Planar two-dimensional flows can only be an approximation of the real world, since no object can be infinitely long in the direction perpendicular to the plane of the picture.
Steady and unsteady flows
At Re=20 the flow past a circular cylinder is steady. This means that the velocity field does not change in time. In steady flows fluid particles move along the streamlines. However, if the flow is unsteady then the streamlines, too, vary with time, and as a result the trajectory of a fluid particle can be different from the instantaneous streamline the particle is on at a particular moment. Unsteady velocity field can be denoted as u(t,x), where t stands for time.
(Italic font is used to distinguish mathematical symbols from ordinary text. Vectors are not in italics because they can be distinguished by bold face.)
Fluid-dynamics terminology is extensive. More terms will be explained in other pages.