Hydrodynamics is the name of the branch of fluid dynamics that considers incompressible flows.
Pressure and friction are forces acting in fluid. Everyone has experienced pressure in the everyday life. When a strong wind breaks down an umbrella, this happens because the pressure on one side of the umbrella cloth is much higher than the pressure on the other side. The pressure difference can be created by the flow of fluid, and it can cause the fluid to flow.
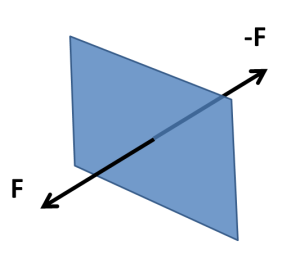
To be precise, pressure is a force per unit area. Imagine a small surface element inside the fluid (see the figure). The fluid on one side of this element can exert, though the element, a force on the fluid on the other side. By Newton’s third law the fluid on the other side will, of course, exert an equal and opposite force through the same surface. Pressure is the force divided by the area of the surface element. Since pressure can change from point to point, the element has to be small, so that the variation of pressure over the element could be neglected.
Pressure has three specific properties, which allow to distinguish it from friction. First, unlike the friction force, pressure can be nonzero even if the fluid is at rest. Consider the air inside the air balloon, for example: the fluid does not move, but the pressure is there. Second, pressure is isotropic. This means that the pressure force acts equally in all directions. If the element in the figure was turned by any angle, the pressure force acting through it would be the same. Third, pressure force is always perpendicular to the surface.
If the pressure on one side of a fluid volume is greater than the pressure on the other side of it, the difference in forces might cause the fluid volume to accelerate. Hence, in order to predict how the fluid will move one needs to know what the pressure is going to be. This turns out to be not so easy.
Let us say that we know the entire state of the flow at a certain point in time that is that we know the velocity, pressure, and all other relevant quantities at every point in the flow domain. We want to predict the flow state that will appear shortly afterwards.
For velocity this is easy. Since we know the pressure and friction, we know the force acting on fluid volumes, and since we know the density, we know the mass of the fluid in these volumes. Hence, by Newton’s second law, we know the acceleration, that is the rate of change of velocity. After a short time interval the velocity will change by the amount equal to the product of acceleration and the length of the time interval.
The displacement of fluid particles over a short time interval is easy to predict when their velocity is known. In the case of a compressible flow one can then figure out how the density of the fluid will change. One can also figure out how the temperature will change (here we will not discuss how). Then one can use the gas law to calculate the pressure. However, for an incompressible fluid this is overkill: it is too hard, and it is unnecessary. After all, the density of incompressible fluid is constant, and this is a significant simplification. What about predicting the pressure, then?
In an incompressible fluid the velocity field is constrained by the requirement that the motion of the fluid particles does not change the fluid volume, as we have already discussed in the Incompressibility section. This also constraints the acceleration: the velocity can vary with time but the new velocity field also has to satisfy the incompressibility requirement. Hence, the answer is that the pressure field should be such that the resulting acceleration field would not violate incompressibility. Mathematically, this is the constraint that allows to calculate the pressure. But is this simple, at the intuitive level? No!
There are two major ways out of all this complexity. Instead of considering the coupled velocity and pressure fields one can abandon pressure at all, and consider instead the coupled velocity and vorticity field. It turns out to be much easier. Second, the problem of determining the pressure for a given velocity field becomes much easier for the case when friction can be neglected. Friction can often be neglected in large part of the flow domain. In the remaining part, consisting of thin boundary layers and shear layers, the pressure is the same as in the surrounding areas.
This way of reasoning, in terms of vorticity-velocity instead of pressure-velocity, and in terms of boundary layers when possible, is the key to intuitive understanding of hydrodynamics. It is this way of reasoning that we will try to develop in the follow-on sections.
As an example of this way of reasoning consider the Bathtab vortex and the Kelvin-Helmholtz instability pages on our website.
