Previous page
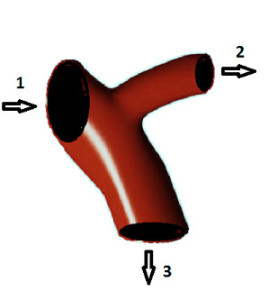 Everyone knows that mass is conserved. What does this mean for a fluid flow? Consider a branched pipe shown in the figure. Suppose that a fluid is flowing through it as shown with arrows. Then mass conservation means that the rate, with which the mass of the fluid inside the pipe varies is the difference between the rate with which the fluid carries mass through inlet 1, and the sum of the rates with which the fluid carries mass through outlets 2 and 3.
Everyone knows that mass is conserved. What does this mean for a fluid flow? Consider a branched pipe shown in the figure. Suppose that a fluid is flowing through it as shown with arrows. Then mass conservation means that the rate, with which the mass of the fluid inside the pipe varies is the difference between the rate with which the fluid carries mass through inlet 1, and the sum of the rates with which the fluid carries mass through outlets 2 and 3.
The mass of the fluid inside the pipe equals the product of the fluid density and the volume of the fluid inside the pipe. Since the volume does not vary with time, the rate with which the mass of the fluid inside the pipe varies is proportional to the rate with which the density of the fluid inside the pipe varies. If the density variation can be neglected, it is very convenient, because it simplifies the matter.
Fluids of constant density are called incompressible fluids. In particular, for an incompressible fluid we can say that the rate with which the fluid carries mass through inlet 1 equals the sum of the rates with which the fluid carries mass through outlets 2 and 3. This is true even when the flow rates vary with time. The mass flow rate through a cross-section of a pipe is the product of the fluid density, average velocity component perpendicular to the cross-section, and the cross-section area. Using the subscript to denote the quantity at the corresponding cross-section and taking into account that the density is the same everywhere, mass conservation gives
v1 A1 =v2 A2 + v3 A3,
where A stands for the cross-section area and v is the velocity across it. This is, indeed, simple.
Under normal conditions density variation of the density of liquids, such as water, can indeed be neglected. For gases, such as air, this is more complicated. However, if the variation of the absolute pressure and the absolute temperature of the gas can be neglected, then from the gas laws it follows that the density variation can also be neglected.
Pressure and density variation can be due to various reasons. For example, air can be pumped into a car tire to the pressure of 2 atm, while on the outside the absolute pressure is 1 arm. If now we can bleed the air from the tire, the air pressure will change by the factor of two, and, therefore, in such a flow one cannot assume the air to be incompressible. Similarly, large temperature variation can be caused by direct heating, thus also leading to the violation of incompressibility assumption.
Variation of pressure and temperature can be caused by the flow itself. The theory of compressible flows shows that the relative magnitude of these variations is of the same order as the Mach number squared. The Mach number M is the ratio of the characteristic flow velocity to the speed of sound. Under normal conditions in the air the speed of sound is about 340 m/s (or about 1,200 kilometres per hour, or 770 mph). Incompressible flow assumption is usually considered to be valid for M<0.3.
Although rare, there are flows in which the free path of the molecules is not small enough as compared to the characteristic dimensions of the flow. This might be the case for spaceships in the upper atmosphere and for flows in very thin tubes, as encountered in nanotechnology or medical applications. In this case the assumption of continuum media does not work.
If, however, the fluid can be considered as a continuum, the Mach number is less than 0.3, and the relative variation of absolute pressure and temperature due to external reasons is small enough then the fluid flow can be considered as a flow of an incompressible fluid. (Small enough means that the acceptable error is noticeably greater than the relative variation of absolute pressure and temperature).
It is useful to know that mathematically the property of incompressibility of the vector field u can be expressed as
∇· u = 0.
This is called the continuity equation for an incompressible fluid. In what follows we will, however, use only the intuitive understanding of incompressibility but not the above equation.
From now on we will consider only incompressible fluids.
